我复习期末的时候还是觉得特征线法很难受,而在波动方程这一部分中它又老出现,和什么riemann invariant搅在一起让人头疼,所以觉得应该写一个笔记。希望能从一个比较具象的角度理解它。这个东西很多地方也不教,默认大家都觉得很平凡,也许还是应该教一下的。还有波这个主题,有的时候我怀疑自己脑子里面缺一些结构,大家都默认波动很简单,可是我很难具体地想象出波来,更不用说波动方程玩出花的各种解了。
线性情形
考虑
$\boldsymbol{\alpha}(\boldsymbol{x}, u) \cdot \frac{\partial}{\partial \boldsymbol{x}} u=\beta(\boldsymbol{x}, u)$
引入时间$s$,使得其解如同流线
$\frac{d u}{d s}=\frac{\partial u}{\partial \boldsymbol{x}} \cdot \frac{d \boldsymbol{x}}{d s}$
这流线就是特征线。然后对号入座,比较系数。例如从方程
$\frac{\partial u}{\partial t}+x \frac{\partial u}{\partial x}=u^{2}, \quad u(x, 0)=f(x)$
就可以得到
$d t=\frac{d x}{x}=\frac{d u}{u^{2}}$
使得其能够方便解出。知道一条特征线上的一点的解,就可以沿着特征线propagate,得到这条线上其他点处的解。
一阶PDE
考虑方程
$F\left(\boldsymbol{x}, u, \frac{\partial u}{\partial \boldsymbol{x}}\right)=const.$
记
$\boldsymbol{p}=\frac{\partial u}{\partial \boldsymbol{x}}$
得到
$\begin{aligned} 0 &=\frac{\partial F}{\partial \boldsymbol{x}} \cdot \frac{d \boldsymbol{x}}{d s}+\frac{\partial F}{\partial u} \frac{\partial u}{\partial \boldsymbol{x}} \cdot \frac{d \boldsymbol{x}}{d s}+\frac{\partial F}{\partial \boldsymbol{p}} \cdot \frac{d \boldsymbol{p}}{d s} \\&=\left(\frac{\partial F}{\partial \boldsymbol{x}}+\frac{\partial F}{\partial u} \boldsymbol{p}\right) \cdot \frac{d \boldsymbol{x}}{d s}+\frac{\partial F}{\partial \boldsymbol{p}} \cdot \frac{d \boldsymbol{p}}{d s}\end{aligned}$
我们为了达成这个条件,指定
$\frac{d \boldsymbol{x}}{d s}=\frac{\partial F}{\partial \boldsymbol{p}}, \quad \frac{d \boldsymbol{p}}{d s}=-\frac{\partial F}{\partial \boldsymbol{x}}-\frac{\partial F}{\partial u} \boldsymbol{p}$
为了表示出我们对p的定义,写下
$\frac{d u}{d s}=\frac{\partial u}{\partial \boldsymbol{x}} \cdot \frac{d \boldsymbol{x}}{d s}=\boldsymbol{p} \cdot \frac{\partial F}{\partial \boldsymbol{p}}$
放在一起得到
$\left\{\begin{aligned} \frac{d \boldsymbol{x}}{d s} &=\frac{\partial F}{\partial \boldsymbol{p}} \\ \frac{d \boldsymbol{p}}{d s} &=-\frac{\partial F}{\partial \boldsymbol{x}}-\frac{\partial F}{\partial u} \boldsymbol{p} \\\frac{d u}{d s} &=\boldsymbol{p} \cdot \frac{\partial F}{\partial \boldsymbol{p}} \\ F(\boldsymbol{x}, u, \boldsymbol{p}) &=0 \end{aligned}\right.$
这个形式非常眼熟,使人想到哈密顿力学。将$\boldsymbol{x}$换成$\boldsymbol{q}$,F换成H,我们就得到
$\left\{\begin{aligned} \frac{dH(\boldsymbol{p}, \boldsymbol{q}, S)}{dt}=\frac{\partial H}{\partial t}&=0\\\frac{\partial H}{\partial S}&=0 \end{aligned}\right.$
其中S是作用量。
不止一阶的PDE
cauchy data
我很粗略地理解为,给定某个条件,能够通过在特征线上的propagation把方程解出来的话,这条件就算是cauchy data。反例比如热传导方程
$\frac{\partial \phi}{\partial t}=\kappa \frac{\partial^{2} \phi}{\partial x^{2}}$
常常会带着的初值条件
$\phi(x, t=0)$
因为$t=0$本来就是一条特征线。你没法从这个条件在特征线上的传导得知其他时刻的热的分布。
达朗贝尔解
考虑波动方程
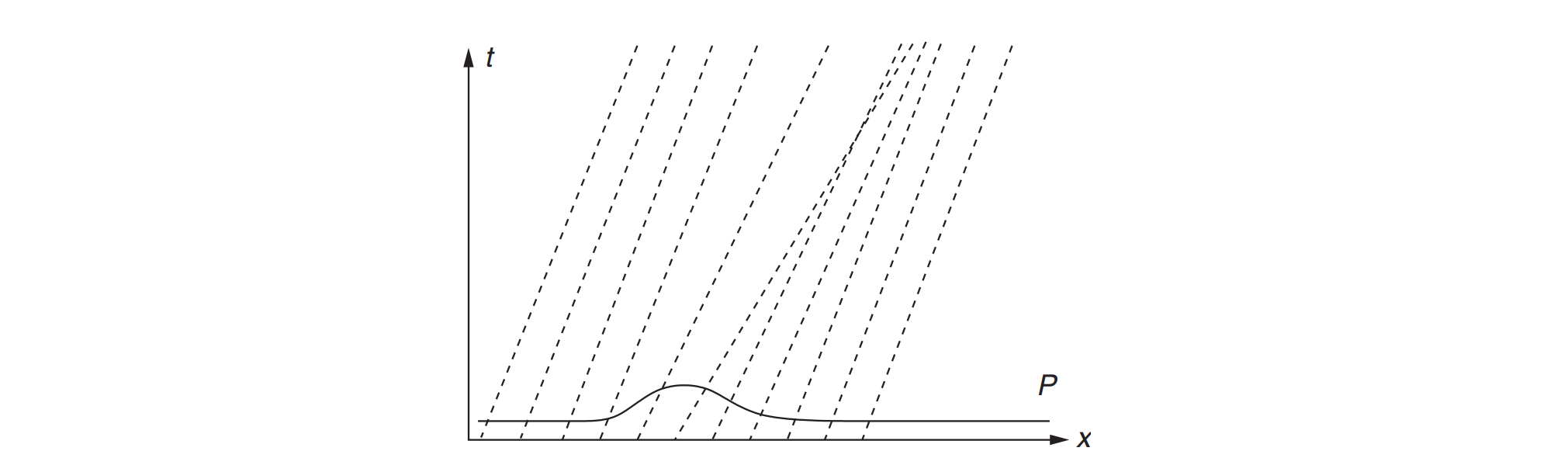
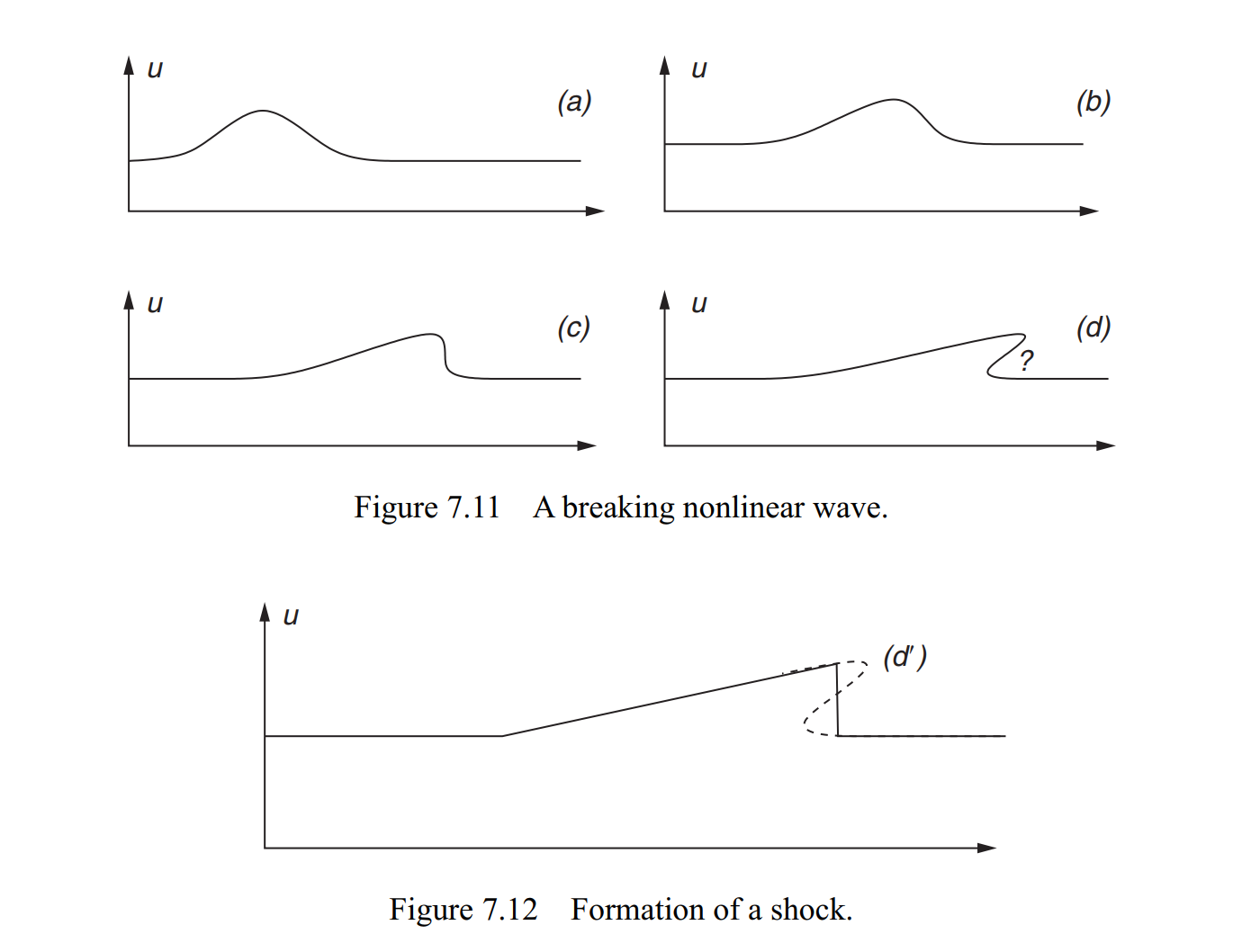
$\frac{\partial^{2} \varphi}{\partial x^{2}}-\frac{1}{c^{2}} \frac{\partial^{2} \varphi}{\partial t^{2}}=0, \quad-\infty 它的性质很好,可以因式分解 $0=\left(\frac{\partial^{2} \varphi}{\partial x^{2}}-\frac{1}{c^{2}} \frac{\partial^{2} \varphi}{\partial t^{2}}\right)=\left(\frac{\partial}{\partial x}+\frac{1}{c} \frac{\partial}{\partial t}\right)\left(\frac{\partial \varphi}{\partial x}-\frac{1}{c} \frac{\partial \varphi}{\partial t}\right)$ 就得到两组特征线$x\pm ct=const. $ 从这可以得出达朗贝尔解 $\varphi(x, t)=\frac{1}{2}\left\{\varphi_{0}(x+c t)+\varphi_{0}(x-c t)\right\}+\frac{1}{2 c} \int_{x-c t}^{x+c t} v_{0}(\xi) d \xi$ 从这个解的形式可以看出来相空间中某一点的值是由哪些点决定的,又能影响得到哪些点。实际上尽管不同组的特征线现在相交了,同一组的特征线还是不相交的。 我觉得可以把这东西理解成一个非相对论版本的光锥。 相速度是振动形式传播的速度。群速度是振动本身传播的速度。振动本身传播的速度可以理解为振动的能量传播的速度,即振幅的变化传播的速度。振幅的变化的传播就是波包的传播,因此群速度就是波包传播的速度。例如,我持续用力振动绳索的一头,此时从我手臂振动的信息与绳子的参数可以得到相速度,而绳子中振动部分与平稳部分分界处的移动速度是群速度,它是仅从绳子本身的信息得到的。 在中学里面我们知道相速度$v_p=\omega/k$。对于群速度,考虑波包 $\varphi(x, t)=\int_{-\infty}^{\infty} \frac{d k}{2 \pi} A(k) e^{i t \psi(k)}$ 其中 $\psi(k)=k\left(\frac{x}{t}\right)-\omega(k)$ 其中心处满足 $\frac{d \psi}{d k}=0$ 不然,当t极大而x与其同尺度时,k的小变化将引起傅里叶展开的各项相消,导致振幅消失。上式即给出群速度的公式 $v_{g}=\frac{\partial \omega}{\partial k}$ 在知乎上,我看到一个答案,指出这个简洁的办法是费米给出的。 关系$\omega=\omega(k)$称为色散关系。在波动力学里面,由于$\omega,k$分别同能动量对应,因此色散关系对应能动量关系,决定了系统的能级分布,进而决定了物质的许多性质。 Michael Stone大概是威尔士人。他教材的例题插图里面居然有一列火车,上印“Rheil Cymru”,或“Wales Rails”。 波阻指的是物体在介质里运动时,由于其速度超过声速而受到的阻力。这阻力是与粘滞阻力独立的。我们使用“威尔士铁路”习题来了解一下它是怎样产生的: 这列火车上方有线缆,“电刷”在线缆上激起一个扰动,因此产生一个波。在火车上看,这个波是驻波(想一下,刷头处一直是顶着的,这个位置振幅一直不变。这也意味着相速度和火车车速是一样的)。因此,把这个波的解写成$y(x-U t)$。我们写线缆的“声”速是$c=\sqrt{T / \rho}$,我们认为线缆是有重量的,于是可以用经典Klein-Gordon方程描绘线缆的振动 $\rho \ddot{y}-T y^{\prime \prime}+\rho \Omega^{2} y=F \delta(x-U t)$ 如果车速低于线缆音速,那么可以改写 $-y^{\prime \prime}+\frac{\gamma^{2} \Omega^{2}}{c^{2}} y=\frac{\gamma^{2} F}{T} \delta(x-U t)$ 其中$\gamma^{2}=\left(1-U^{2} / c^{2}\right)^{-1}$。这解出来是个指数函数的形式: $y(x, t)=\frac{\gamma^{2} F}{T}\left(\frac{c}{2 \Omega \gamma}\right) \exp \left\{-\frac{\Omega \gamma}{c}|x-U t|\right\}$,即使在左边也会很快衰减到0. 如果车速高于线缆音速,那么则是 $-y^{\prime \prime}-\frac{\tilde{\gamma}^{2} \Omega^{2}}{c^{2}} y=\frac{\tilde{\gamma}^{2} F}{T} \delta(x-U t)$ 其中$\tilde{\gamma}^{2}=\left(U^{2} / c^{2}-1\right)^{-1}$。这解出来则是正弦形式的 $y(x, t)=\left\{\begin{array}{ll}{\frac{\tilde{\gamma}^{2} F}{T}\left(\frac{c}{\Omega \tilde{\gamma}}\right) \sin \left(\frac{\Omega \tilde{\gamma}}{c}(U t-x)\right),} & {xU t}\end{array}\right.$ 这个拖在火车后面的正弦波学名叫wake,我也不知道中文是啥。总之,在这种情况下,可以算出来这个wake单位长度的能量密度 $\begin{aligned} \mathcal{E} &=\frac{1}{2} \rho \dot{y}^{2}+\frac{1}{2} T\left(y^{\prime}\right)^{2}+\frac{1}{2} \rho \Omega^{2} y^{2} \\ &=\rho\left(\frac{\tilde{\gamma}^{2} F}{T}\right)^{2} U^{2} \sin ^{2}\left(\frac{\Omega \tilde{\gamma}}{c}|x-U t|\right) \end{aligned}$ $\langle\mathcal{E}\rangle=\frac{1}{2} \rho \tilde{\gamma}^{4}\left(\frac{F}{T}\right)^{2} U^{2}$ 这个能量是以群速度向前传播的。然而,火车的速度比这要更快,因此火车不断地消耗其发动机做的功,用来补这个wake的能量。这相当于有一个恒定的阻力作用在火车上面: $ UF_{drag}=\langle\mathcal{E}\rangle\left(U-U_{g}\right)$ (从Klein-Gordon方程的色散关系可以算出群速度。) 当然,这个阻力只有在$U>c$的时候才会出现。 在流体中,由质量守恒 $\partial_{t} \rho+\partial_{x}(\rho v)=0$ 和牛顿第二定律 $\rho\left(\partial_{t} v+v \partial_{x} v\right)=-\partial_{x} P$ 以及声速 $c^{2}=\frac{d P}{d \rho}$ 研究声音的传播,时,黎曼定义了一个热力学量 $\pi=\int_{P_{0}}^{P} \frac{1}{\rho c} d P$ 并且写出方程 $\partial_{t}(v+\pi)+(v+c) \partial_{x}(v+\pi)=0$ 对此,知道黎曼不变量$v \pm \pi$在两组特征线$\frac{d x}{d t}=v \pm c$上是定值。 然而,如果声速随压强改变(非线性性),那么这些特征线就会相交,造成问题。下图展示了这种情况下产生激波的过程。 存在色散和非线性性的情况下,一般波包会很快消失掉。假设有一介质,如某种玻璃,其中色散关系使得不同频率的成分,其群速度不同,那么波包不能长久。但如果使得各成分的振幅符合特定关系,使得介质的非线性性对于折射率的影响弥补了色散的影响,那么此波包各成分的速度仍旧相等,而波包能够保持不散。这种解就是孤子。 孤子和激波都是十分有趣的对象,迫于时间、能力和傻逼typora吞我内容的缘故,我不能对这两类解说得更多了(反正也不会考。。。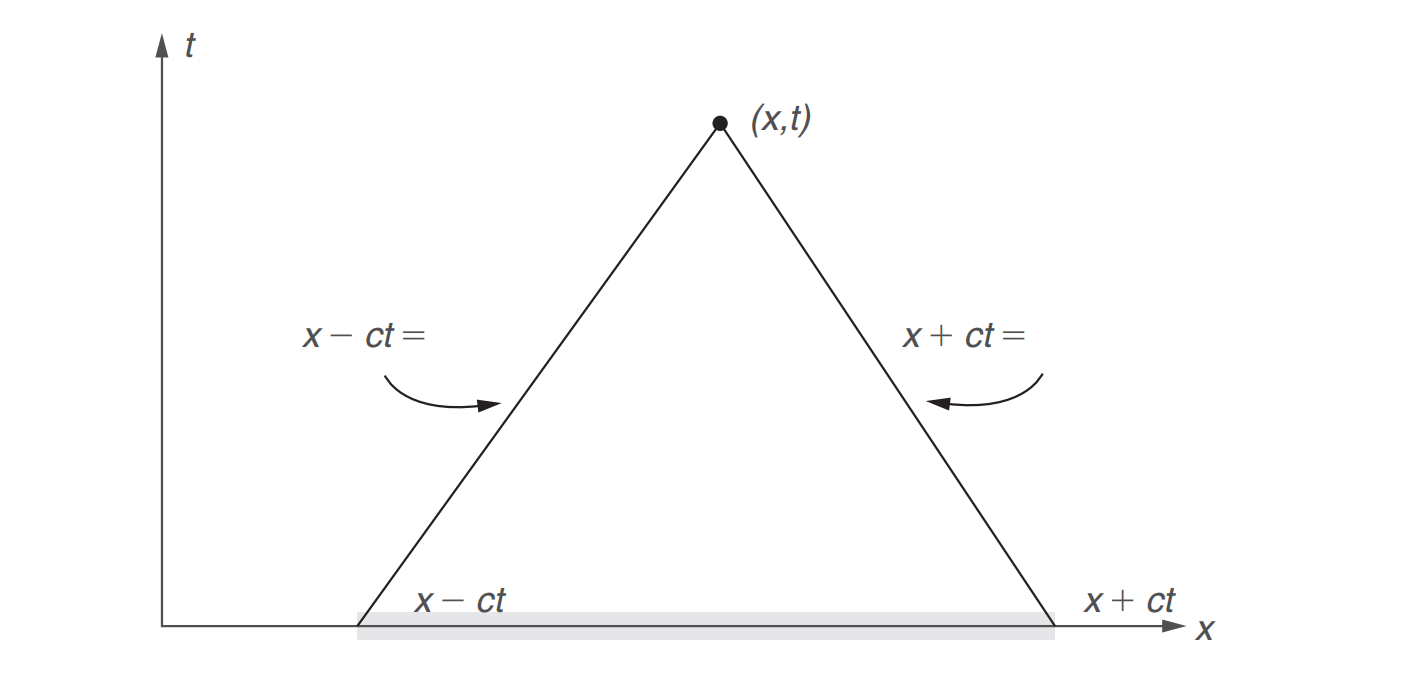
色散关系
波阻

激波和孤子
$\partial_{t}(v-\pi)+(v-c) \partial_{x}(v-\pi)=0$