关于PDE,我的问题是缺乏一种系统的把握。我所有的训练都是在数理方程的课上得到的,这些训练只告诉我某些十分特定的方程的解是某些特殊函数,至于这些方程的特定究竟特定到了什么程度,具体是怎样的条件,虽然也讲,但并不重视,主要重视的是造成这些方程的物理问题。所以就形成一个对物理问题的解的感觉。但是这个感觉现在也已经消退了。所以要重新从这些基础的东西学起。
分类
物理上主要是考虑二阶PDE,比如说双曲型的波动方程,椭圆形的泊松方程,抛物线型的导热方程。然后边界条件也主要见到三类,dirichlet给定边界的函数值,neumann条件给定边界的导数,cauchy两者都给定。实际上解决问题的时候,有唯一解的必要条件对于椭圆和抛物型方程来说是边界条件有d和n的其中之一,而对双曲型,则得是c。
Cauchy data
一维最简单的情况,知道位置和速度,就能推演以后的运动。这个时候这两个信息就是cauchy data。二维的时候
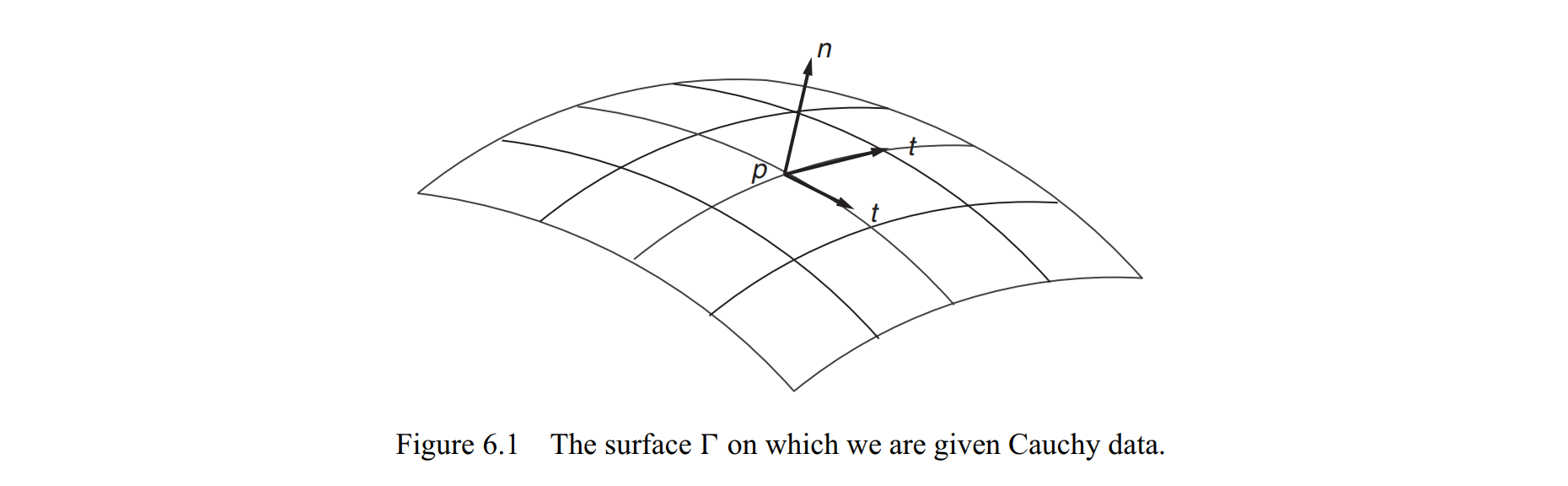
我们给一个曲面,上面的函数值和导数是知道的,原则上
$\begin{aligned} \frac{\partial^{2} \varphi}{\partial n \partial t_{i}} & \stackrel{\text { def }}{=} n^{\mu} t_{i}^{\nu} \frac{\partial^{2} \varphi}{\partial x^{\mu} \partial x^{\nu}} \\ \frac{\partial^{2} \varphi}{\partial t_{i} \partial t_{j}} & \stackrel{\text { def }}{=} t_{i}^{\nu} t_{j}^{\nu} \frac{\partial^{2} \varphi}{\partial x^{\mu} \partial x^{\nu}} \end{aligned}$
是知道的,但就这些还求不出jacobian的全部信息,还得要知道
$\frac{\partial^{2} \varphi}{\partial n \partial n} \stackrel{\operatorname{def}}{=} n^{\mu} n^{\nu} \frac{\partial^{2} \varphi}{\partial x^{\mu} \partial x^{\nu}}$
才行。求这个东西的trick是取$\frac{\partial^{2} \varphi}{\partial x^{\mu} \partial x^{\nu}}=\phi_{0}^{\mu \nu}+n^{\mu} n^{\nu} \Phi$,其中$\phi$是满足前两组方程的解,$\Phi$是这个解之外的“正交”的部分。对于方程
$a_{\mu \nu}(x) \frac{\partial^{2} \varphi}{\partial x^{\mu} \partial x^{\nu}}+(\text { lower orders })=0$
我们就知道
$a_{\mu \nu}\left(x_{i}\right) \frac{\partial^{2} \varphi}{\partial x^{\mu} \partial x^{\nu}}+(\text { known lower orders })=0$
$a_{\mu \nu} n^{\mu} n^{\nu} \Phi+(\mathrm{known stuff})=0$
如果$a_{\mu \nu} n^{\mu} n^{\nu}$是0的话就坏了,我们就求不出来$\Phi$了。对于这种的点我们叫characteristic (surface),因为它老是连成面。以后我就管他叫char。char对解方程其实是有好处的,不是完全的坏事。关于解的信息可以在char上面传递。看一个例子:
$a(x, y) \frac{\partial u}{\partial x}+b(x, y) \frac{\partial u}{\partial y}+c(x, y) u=f(x, y)$
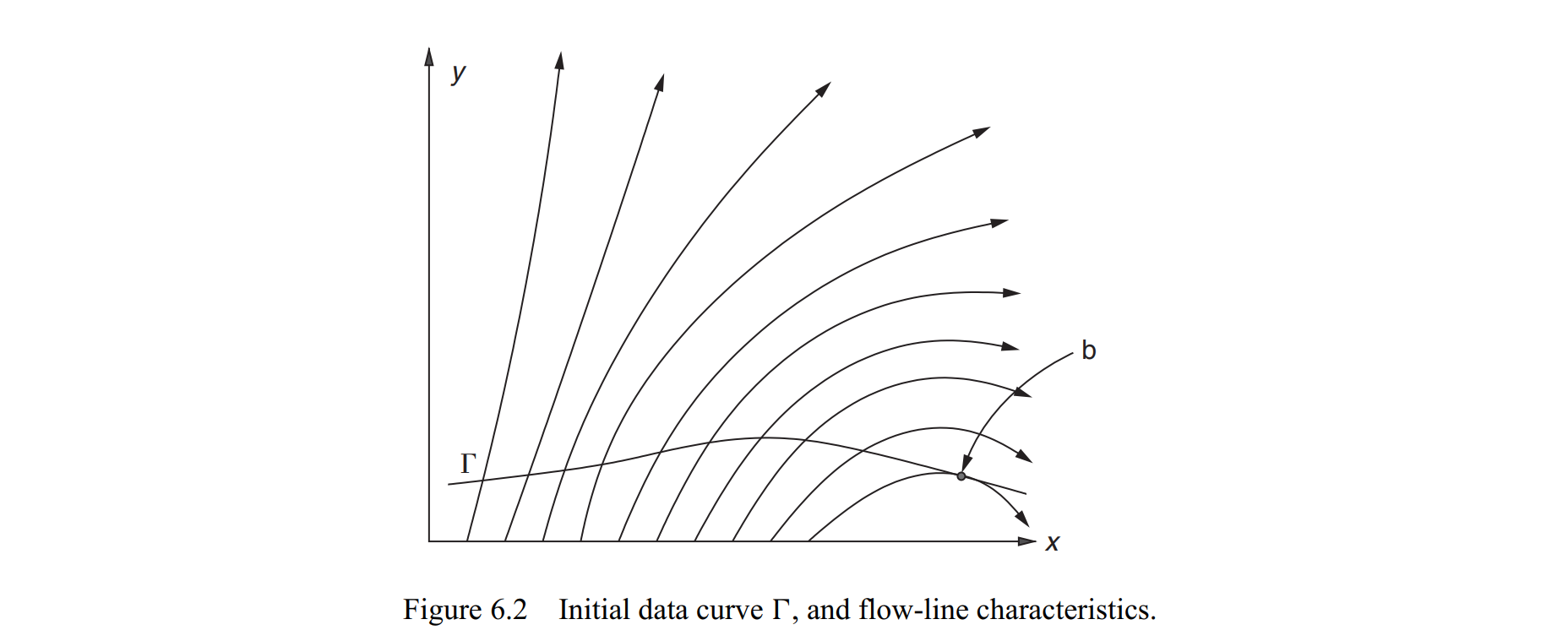
它是$(\mathbf{v} \cdot \nabla) u+c u=f$式的方程,给出一个u的流。每条流线上$\frac{d u}{d t}+c(t) u(t)=f(t)$,其中t是使得$\frac{d x}{d t}=a(x, y), \quad \frac{d y}{d t}=b(x, y)$的的参数化。给一条线$\Gamma$上的cauchy data,这个线和流线(也就是char)相交的点处的信息全知道,所以每条char上面的结果都能解出来。如果相切了,那多半就是无解。
波动方程
一、
波动方程是一个二阶的双曲方程。这种方程高次项可以因式分解
$\begin{aligned} a \frac{\partial^{2}}{\partial x^{2}}+2 b \frac{\partial^{2}}{\partial x \partial y}+c \frac{\partial^{2}}{\partial y^{2}} &=\left(\alpha \frac{\partial}{\partial x}+\beta \frac{\partial}{\partial y}\right)\left(\gamma \frac{\partial}{\partial x}+\delta \frac{\partial}{\partial y}\right)+\text { lower, } \\ &=\left(\gamma \frac{\partial}{\partial x}+\delta \frac{\partial}{\partial y}\right)\left(\alpha \frac{\partial}{\partial x}+\beta \frac{\partial}{\partial y}\right)+\text { lower. } \end{aligned}$
然后写成
$\left(\alpha \frac{\partial}{\partial x}+\beta \frac{\partial}{\partial y}\right) U_{1}+F_{1}=0$
$\left(\gamma \frac{\partial}{\partial x}+\delta \frac{\partial}{\partial y}\right) U_{2}+F_{2}=0$
当做一维的PDE来求解。波动方程就可以这样解。还有一个简单的办法是d’Alambert弄出来的,令
$\xi=x+c t$
$\eta=x-c t$
就知道
$\frac{\partial}{\partial \xi}=\frac{\partial x}{\partial \xi} \frac{\partial}{\partial x}+\frac{\partial t}{\partial \xi} \frac{\partial}{\partial t}=\frac{1}{2}\left(\frac{\partial}{\partial x}+\frac{1}{c} \frac{\partial}{\partial t}\right)$
$\frac{\partial}{\partial \eta}=\frac{1}{2}\left(\frac{\partial}{\partial x}-\frac{1}{c} \frac{\partial}{\partial t}\right)$
$\left(\frac{\partial^{2}}{\partial x^{2}}-\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}}\right)=\left(\frac{\partial}{\partial x}+\frac{1}{c} \frac{\partial}{\partial t}\right)\left(\frac{\partial}{\partial x}-\frac{1}{c} \frac{\partial}{\partial t}\right)=4 \frac{\partial^{2}}{\partial \xi \partial \eta}=0$
所以说
$\varphi(x, t)=f(\xi)+g(\eta)=f(x+c t)+g(x-c t)$。
现在我们有初值$\varphi(x, 0) \equiv \varphi_{0}(x)$ and $\dot{\varphi}(x, 0) \equiv v_{0}(x)$,这个就是cauchy data。我们就知道
$\begin{aligned} f(x)+g(x) &=\varphi_{0}(x) \\ c\left(f^{\prime}(x)-g^{\prime}(x)\right) &=v_{0}(x) \end{aligned}$
以下这个积分的过程相当于是把解的信息在char上propagate:
$f(x)-g(x)=\frac{1}{c} \int_{0}^{x} v_{0}(\xi) d \xi+A$
然后就一路得到结果。
二、
还有一种办法可以展示积分变换怎样解这个问题:做Fourier变换
$\varphi(x, t)=\int_{-\infty}^{\infty} \frac{d k}{2 \pi}\left\{a(k) e^{i k x-i \omega_{k} t}+a^{*}(k) e^{-i k x+i \omega_{k} t}\right\}$
边界条件
$\Phi(k) \stackrel{\text { def }}{=} \int_{-\infty}^{\infty} \varphi(x, t=0) e^{-i k x} d x$
$\chi(k) \stackrel{\text { def }}{=} \int_{-\infty}^{\infty} \dot{\varphi}(x, t=0) e^{-i k x} d x$
对应
$\Phi(k)=a(k)+a^\*(-k)$
$\chi(k)=i \omega_{k}\left(a^{\*}(-k)-a(k)\right)$
然后就知道结果了。
三、
格林函数作为另外一种具备普遍性的办法,可以解这个问题。对于有源的方程
$\frac{1}{c^{2}} \frac{\partial^{2} \varphi}{\partial t^{2}}-\frac{\partial^{2} \varphi}{\partial x^{2}}=q(x, t)$
我们解
$\left(\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}}-\frac{\partial^{2}}{\partial x^{2}}\right) G(x, t ; \xi, \tau)=\delta(x-\xi) \delta(t-\tau)$
考虑到因果性,我们是在t上面积分,因为$t<\tau$这一段已经知道是0了。
$\begin{aligned} G(x, \tau+\varepsilon ; \xi, \tau) &=0 \\ \frac{d}{d t} G(x, \tau+\varepsilon ; \xi, \tau) &=c^{2} \delta(x-\xi) \end{aligned}$
这就是$\tau$右边这一段的cauchy data。从$f(x+c t)+g(x-c t)$形式的解代入
$\begin{aligned} f(x)+g(x) &=\varphi_{0}(x) \\ c\left(f^{\prime}(x)-g^{\prime}(x)\right) &=v_{0}(x) \end{aligned}$
得出来就是
$\begin{aligned} G(x, t ; \xi, \tau) &=\theta(t-\tau) \frac{c}{2} \int_{x-c(t-\tau)}^{x+c(t-\tau)} \delta(\zeta-\xi) d \zeta \\ &=\frac{c}{2} \theta(t-\tau)\{\theta(x-\xi+c(t-\tau))-\theta(x-\xi-c(t-\tau))\} \end{aligned}$
一个算例:不同维度上的爆炸
这是一个挺有意思的事情。考虑三维的一个声波
$\frac{\partial^{2} \phi}{\partial x^{2}}+\frac{\partial^{2} \phi}{\partial y^{2}}+\frac{\partial^{2} \phi}{\partial z^{2}}-\frac{1}{c^{2}} \frac{\partial^{2} \phi}{\partial t^{2}}=0$
把方程写成流方程的形式,就知道一些物理量
$\begin{aligned} v_{1} &=\nabla \phi \\ \rho_{1} &=-\frac{\rho_{0}}{c^{2}} \dot{\phi} \\ P_{1} &=c^{2} \rho_{1} \end{aligned}$
只考虑球面波。直接写
$\phi(r, t)=\frac{1}{r} f\left(t-\frac{r}{c}\right)+\frac{1}{r} g\left(t+\frac{r}{c}\right)$
后一项扔掉,只考虑膨胀。记$\dot{q}$是体积膨胀的速度,$v(r, t)=\frac{\dot{q}(t)}{4 \pi r^{2}}$。那么就有
$\frac{\dot{q}(t)}{4 \pi r^{2}}=v_{1}(r, t)=\frac{\partial \phi}{\partial r}=-\frac{1}{r^{2}} f\left(t-\frac{r}{c}\right)-\frac{1}{r c} f^{\prime}\left(t-\frac{r}{c}\right)$
考虑以下两种情况:
- 近场有$-\frac{1}{4 \pi} \dot{q}(t)=f(t)$
- 远场有$v_{1}=\frac{\partial \phi}{\partial r} \approx-\frac{1}{r c} f^{\prime}\left(t-\frac{r}{c}\right)$
所以实际上由于$\dot{q}(t)$是一个pulse,先增后减的,我们在远场看到的求了导的结果就是先正后负的。
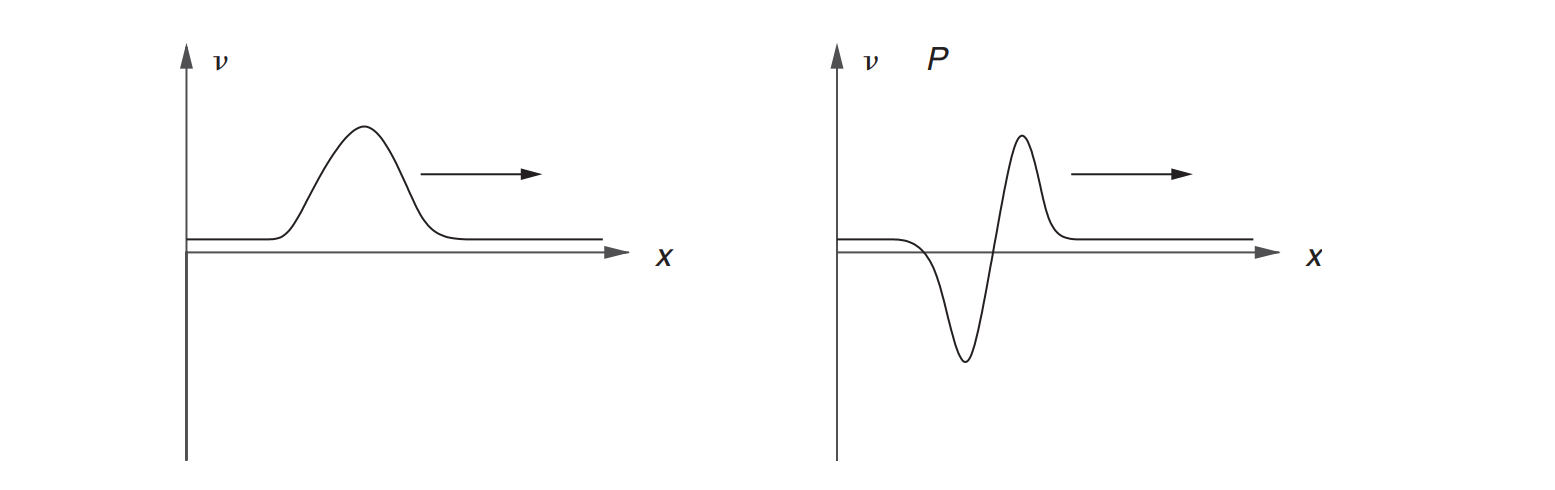
压强也一样。实际上三维的爆炸确实是这样的,外围先往外炸,冲击波过去之后会有负压。这部分低压空气立刻降温,里面的水分就凝结,形成condensation cloud。一些爆炸的照片上可以看到这种现象。
现在换一个情景。
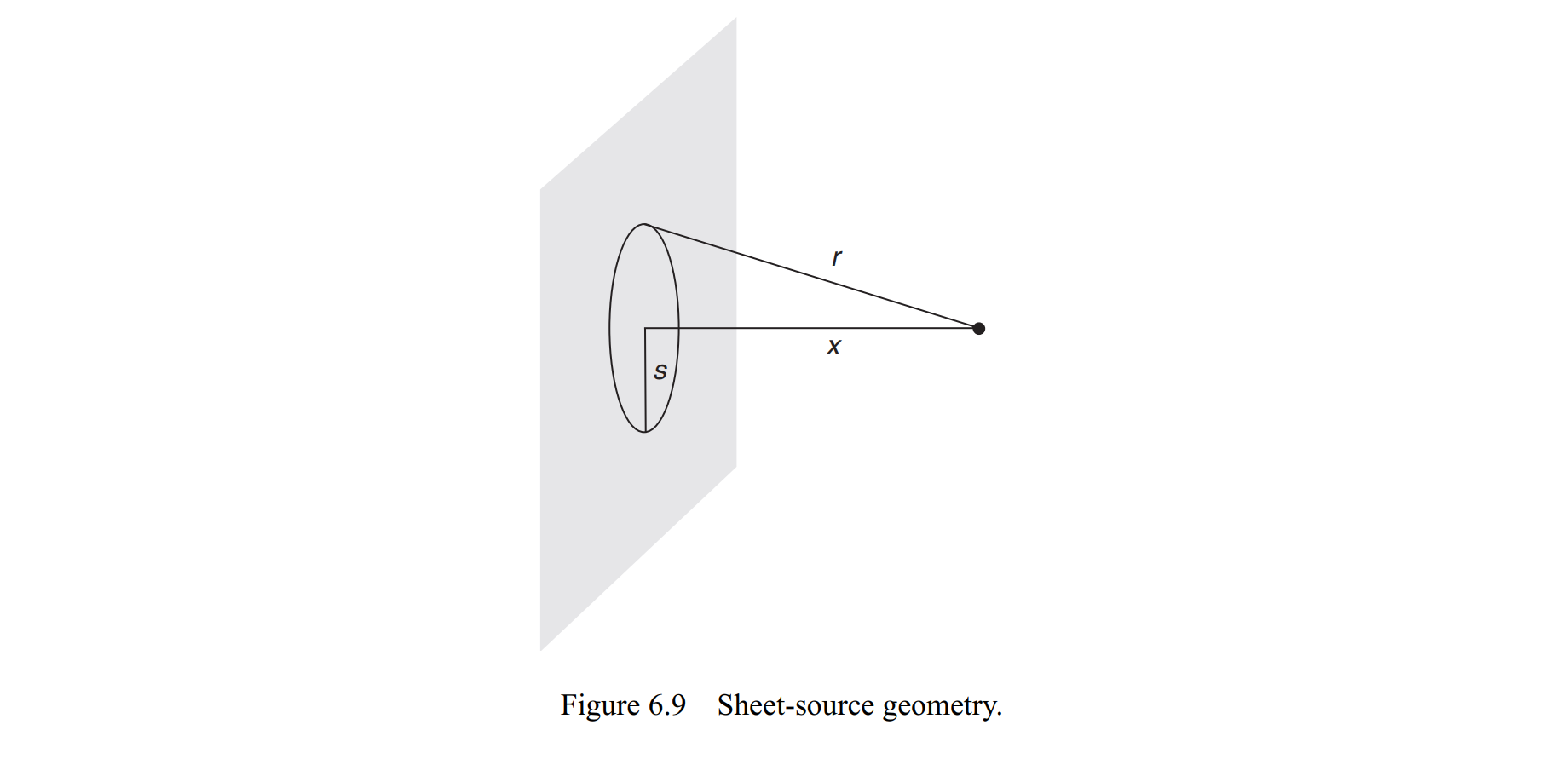
假设有一个二维的圆形爆炸物,炸出来的东西只能在垂直于该炸弹的一维传播。那么,波动方程的解就是
$\phi(x, t)=2 \pi \int_{0}^{\infty} \frac{1}{\sqrt{x^{2}+s^{2}}} f\left(t-\frac{\sqrt{x^{2}+s^{2}}}{c}\right) s d s$
令$\tau=t-\sqrt{x^{2}+s^{2}} / c$,把上式化为
$2 \pi \int_{0}^{\infty} f\left(t-\frac{\sqrt{x^{2}+s^{2}}}{c}\right) d \sqrt{x^{2}+s^{2}}$
$=2 \pi c \int_{-\infty}^{t-x / c} f(\tau) d \tau$
$=-\frac{c}{2} \int_{-\infty}^{t-x / c} \dot{q}(\tau) d \tau$
这个q是单位面积炸出的空间。可以看出来,这回,速度是$v_{1}=\phi^{\prime}(x, t)=\frac{1}{2} \dot{q}(t-x / c)$,远场近场的行为是一样的。
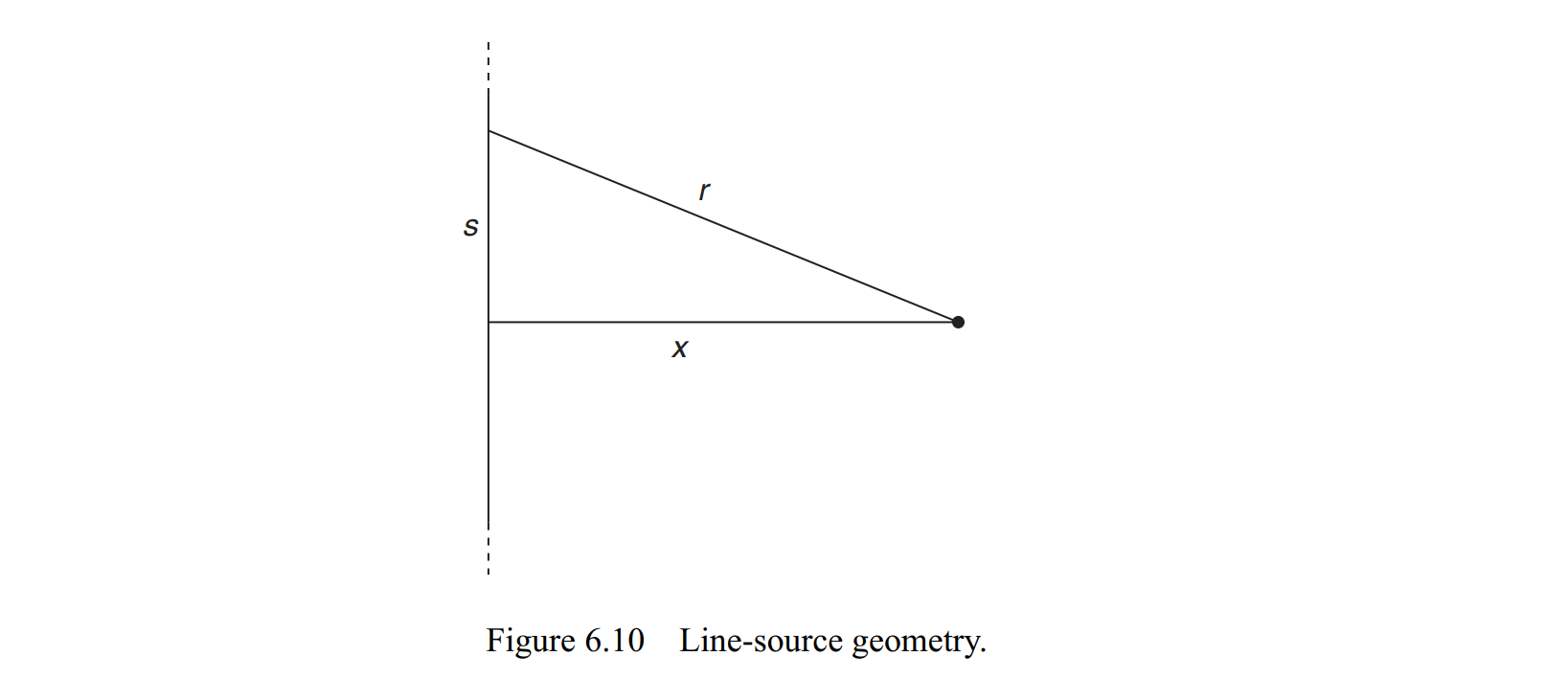
现在,一个最有趣的东西是一维的爆炸物,它的冲击波可以在二维传播。这回,我们有
$\begin{aligned} \phi(x, t) &=\int_{x}^{\infty} \frac{1}{r} f\left(t-\frac{r}{c}\right) \frac{2 r d r}{\sqrt{r^{2}-x^{2}}} \\ &=2 \int_{x}^{\infty} f\left(t-\frac{r}{c}\right) \frac{d r}{\sqrt{r^{2}-x^{2}}} \end{aligned}$
令$\tau=t-r / c$,考虑$f(t)=-\dot{q}(t) / 4 \pi$,$r^{2}-x^{2} \approx 2 x(r-x)$,我们有
$\begin{aligned} \phi(x, t) &=\frac{2 c}{\sqrt{2 x}} \int_{-\infty}^{(t-x / c)} f(\tau) \frac{d r}{\sqrt{(c t-x)-c \tau}} \\ &=-\frac{1}{2 \pi} \sqrt{\frac{2 c}{x}} \int_{-\infty}^{(t-x / c)} \dot{q}(\tau) \frac{d \tau}{\sqrt{(t-x / c)-\tau}} \end{aligned}$
对x求导,得到波速是这样的
$v_{1}(r, t)=\frac{1}{2 \pi c} \sqrt{\frac{2 c}{x}} \int_{-\infty}^{(t-x / c)} \ddot{q}(\tau) \frac{d \tau}{\sqrt{(t-x / c)-\tau}}$
这东西是啥呢?实际上它可以看成是半阶导数。粗略地说,三维爆炸的远场行为是近场行为的一阶导,一维则是零阶导。半阶导怎么定义呢?可以用积分变换的方式:魔改一下拉普拉斯变换
$\left(\frac{d}{d t}\right)^{\frac{1}{2}} F(t) \stackrel{\text { def }}{=} \frac{1}{\sqrt{\pi}} \int_{-\infty}^{t} \frac{\dot{F}(\tau)}{\sqrt{t-\tau}} d \tau$
所以$v_1$实际上对应的是$\dot{q}$的半阶导数。
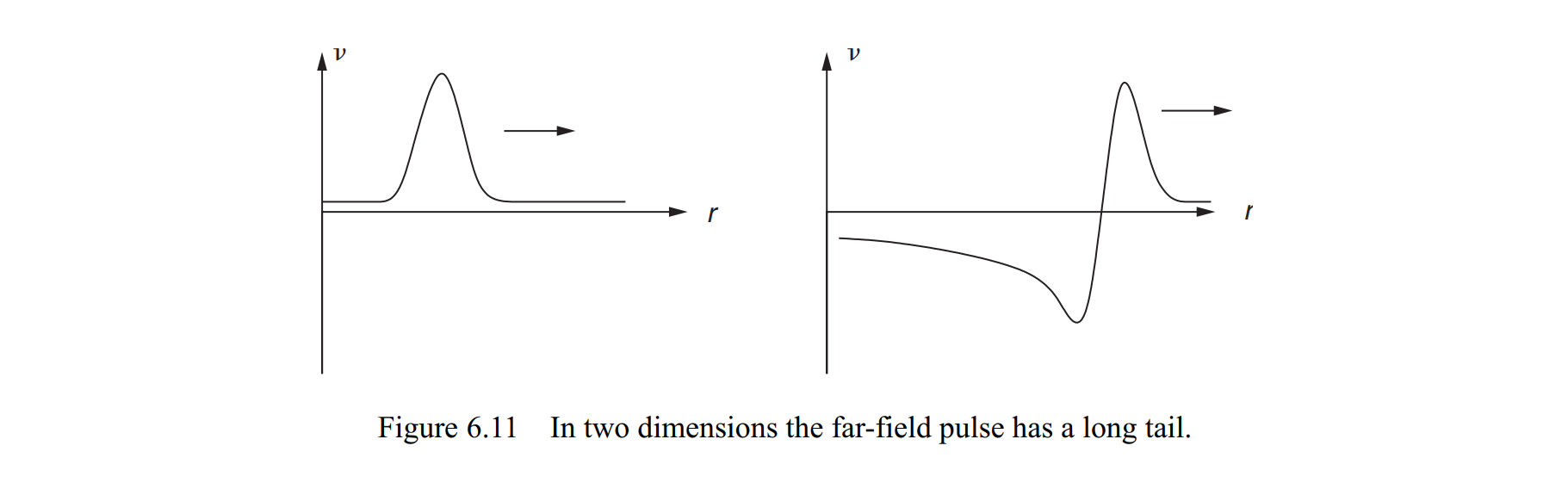
远场行为如图。这玩意一直带一个不会消失的小尾巴,冲击波过了之后,相当于还有源源不断的向里的速度。这是非物理的,并且曾经在某些科学家的研究中造成过困难:一位科学家想要研究一个细长的裂缝导致的地震。他用了一维震源的近似,结果得到了这种非物理结果,害得他浪费大把时间在debug上。此事可引以为戒。
热传导方程
一、
$\frac{\partial \phi}{\partial t}=\kappa \frac{\partial^{2} \phi}{\partial x^{2}}$
可以用傅里叶变换来解:
$\phi(x, t)=\int_{-\infty}^{\infty} \frac{d k}{2 \pi} \tilde{\phi}(k, t) e^{i k x}$
$\frac{\partial \tilde{\phi}}{\partial t}=-\kappa k^{2} \tilde{\phi}$
因此
$\begin{aligned} \phi(x, t) &=\int_{-\infty}^{\infty} \frac{d k}{2 \pi} \tilde{\phi}(k, t) e^{i k x} \\ &=\int_{-\infty}^{\infty} \frac{d k}{2 \pi} \tilde{\phi}(k, 0) e^{i k x-\kappa k^{2} t} \end{aligned}$
就得到一个原理上相当于格林函数的结果
$\begin{aligned} \phi(x, t) &=\int_{-\infty}^{\infty} \frac{d k}{2 \pi}\left(\int_{-\infty}^{\infty} \phi(\xi, 0) e^{i k \xi} d \xi\right) e^{i k x-\kappa k^{2} t} \\ &=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} \frac{d k}{2 \pi} e^{i k(x-\xi)-\kappa k^{2} t}\right) \phi(\xi, 0) d \xi \\ &=\int_{-\infty}^{\infty} G(x, \xi, t) \phi(\xi, 0) d \xi \end{aligned}$
其中格林函数$G(x, \xi, t)=\int_{-\infty}^{\infty} \frac{d k}{2 \pi} e^{i k(x-\xi)-\kappa k^{2} t}=\frac{1}{\sqrt{4 \pi \kappa t}} \exp \left\{-\frac{1}{4 \kappa t}(x-\xi)^{2}\right\}$就是所谓heat kernel。
二、
知乎上有一个民科,个人介绍是杜哈梅原理专家。我才知道杜哈梅就是duhamel,迪亚梅尔。我们先用一个例子看看这个原理的思路。
假设有一个一头受热(热源变温)的棍子,想解这个棍子的传热。这个方程非齐次,不好解。我们先考虑一个满足边界条件$w(0, t)=1$和$w(x, 0)=0$的w,可以解出来是
$w=\theta(t)\left\{1-\operatorname{erf}\left(\frac{x}{2 \sqrt{t}}\right)\right\}$
其中erf是error function $\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-z^{2}} d z$。
现在把每一个时刻的变温写成分立的
$h(t)=\sum_{n} h_{n} \theta\left(t-t_{n}\right)$
或者
$\begin{aligned} h(t) &=h(0)+\int_{0}^{t} \dot{h}(\tau) d \tau \\ &=h(0)+\int_{0}^{\infty} \theta(t-\tau) \dot{h}(\tau) d \tau \end{aligned}$
由于传热方程是线性的,我们可以把每个时刻的解叠加起来,得到原非齐次问题的解
$\begin{aligned} u(x, t) &=\int_{0}^{t} w(x, t-\tau) \dot{h}(\tau) d \tau+h(0) w(x, t) \\ &=-\int_{0}^{t}\left(\frac{\partial}{\partial \tau} w(x, t-\tau)\right) h(\tau) d \tau \\ &=\int_{0}^{t}\left(\frac{\partial}{\partial t} w(x, t-\tau)\right) h(\tau) d \tau \end{aligned}$
所以迪亚梅尔原理就是把非齐次方程变成一堆齐次的初值问题的叠加。
泊松和拉普拉斯方程
Schwinger’s trick
泊松方程的格林函数可以由$g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\sum_{n} \frac{1}{\lambda_{n}} \varphi_{n}(\mathbf{r}) \varphi_{n}^{*}\left(\mathbf{r}^{\prime}\right)$而写成
$g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\int \frac{d^{n} k}{(2 \pi)^{n}} \frac{e^{i \mathbf{k} \cdot\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}}{k^{2}}$
施温格的小技巧可以把这个积分算出来:
$\begin{aligned} g\left(\mathbf{r}, \mathbf{r}^{\prime}\right) &=\int_{0}^{\infty} d s \int \frac{d^{n} k}{(2 \pi)^{n}} e^{i \mathbf{k} \cdot\left(\mathbf{r}-\mathbf{r}^{\prime}\right)} e^{-s k^{2}} \\ &=\int_{0}^{\infty} d s(\sqrt{\frac{\pi}{s}})^{n} \frac{1}{(2 \pi)^{n}} e^{-\frac{1}{4 s}\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{2}} \\ &=\frac{1}{2^{n} \pi^{n / 2}} \int_{0}^{\infty} d t t^{\frac{n}{2}-2} e^{-t\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{2} / 4} \\ &=\frac{1}{2^{n} \pi^{n / 2}} \Gamma\left(\frac{n}{2}-1\right)\left(\frac{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{2}}{4}\right)^{1-n / 2} \\ &=\frac{1}{(n-2) S_{n-1}}\left(\frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}\right)^{n-2} \end{aligned}$
注意到,对$n=2$的情况,这玩意发散。处理办法叫维度正规化,这是QFT里面的一种套路,其要义就是把火苗埋在地毯下面。在n=2附近展开
$\begin{aligned} g\left(\mathbf{r}, \mathbf{r}^{\prime}\right) &=\frac{1}{4 \pi} \frac{\Gamma(n / 2)}{(n / 2-1)}\left(1-(n / 2-1) \ln \left(\frac{1}{4}\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{2}\right)+O\left[(n-2)^{2}\right]\right) \\ &=\frac{1}{4 \pi}\left(\frac{1}{n / 2-1}-2 \ln \left|\mathbf{r}-\mathbf{r}^{\prime}\right|+\cdots\right) \end{aligned}$
现在,我们只要把不取决于位置的$1/(n/2-1)$扫到毯子下面就行了。
惠更斯原理和基尔希霍夫近似
我们在中学都学过惠更斯的波的传播原理。这就是说,下一个时刻的波阵面,取决于上一个时刻波阵面上虚拟波源发出的次波的包络面。这是一个很朴素的想法,甚至21世纪的小学生也能想到。但是,波的传播还有另外一个特性:它能够相干叠加。惠更斯原理没有阐述这一点,而菲涅尔补全了这一部分,他的思路可以作为物理学家的思维方式的范本。
菲涅尔假设波前的任意一点Q在空间点P上贡献的复振幅为$\mathrm{d} \psi\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$。他根据以下直觉作出假设:
- 它正比于波阵面的面源;
- 它正比于r’处的次波源Q的复振幅;
- 它是球面波,$\mathrm{d} \psi\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \propto \frac{e^{i k R}}{R}$;
- 它是各向异性的。假设面元矢量和|r-r’|有夹角$\chi$,那么$\mathrm{d} \psi\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \propto K(\chi)$,即
$\psi(\mathbf{r})=c \oint_{S} \psi\left(\mathbf{r}^{\prime}\right) K(\chi) \frac{e^{i k R}}{R} \mathrm{d} S^{\prime}$
考虑波动方程的格林函数可以用波数作为参数写出来:
$\left[-\nabla^{2}-\left(\frac{\omega^{2}}{c^{2}}\right)\right] G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\delta^{3}\left(\mathbf{r}-\mathbf{r}^{\prime}\right)$
$G_{\pm}\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=\frac{1}{4 \pi\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} e^{\pm i k\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}$
假设在波源处只有向外的波。对于全空间,考虑到波动方程的微分算子是自伴的,使用Lagrange’s Identity(在这个特定的场景下,叫做格林公式):
$\int_{\Omega}\left\{G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)\left(\nabla_{\mathbf{r}}^{2}+k^{2}\right) \psi(\mathbf{r})-\psi(\mathbf{r})\left(\nabla_{\mathbf{r}}^{2}+k^{2}\right) G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)\right\} d^{n} x$
$\quad=\int_{\partial \Omega}\left\{G\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \nabla_{\mathbf{r}} \psi(\mathbf{r})-\psi(\mathbf{r}) \nabla_{\mathbf{r}} G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)\right\} \cdot d \mathbf{S}_{\mathbf{r}}$
我们可以写
$\psi\left(\mathbf{r}^{\prime}\right)=\int_{\partial \Omega}\left\{G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)\left(\mathbf{n} \cdot \nabla_{x}\right) \psi(\mathbf{r})-\psi(\mathbf{r})\nabla_{\mathrm{r}} G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)\right\} d S_{\mathbf{r}}, \quad \mathbf{r}^{\prime} \in \Omega$
从这里其实可以看出来,要解波动方程,诺依曼和狄里赫雷边界条件只能给一个。我们假设从一个一维小孔(实际上就是小缝)里面射出平面波$e^{i k x}$(这意味着,真正产生光的点波源离小孔是很远的),
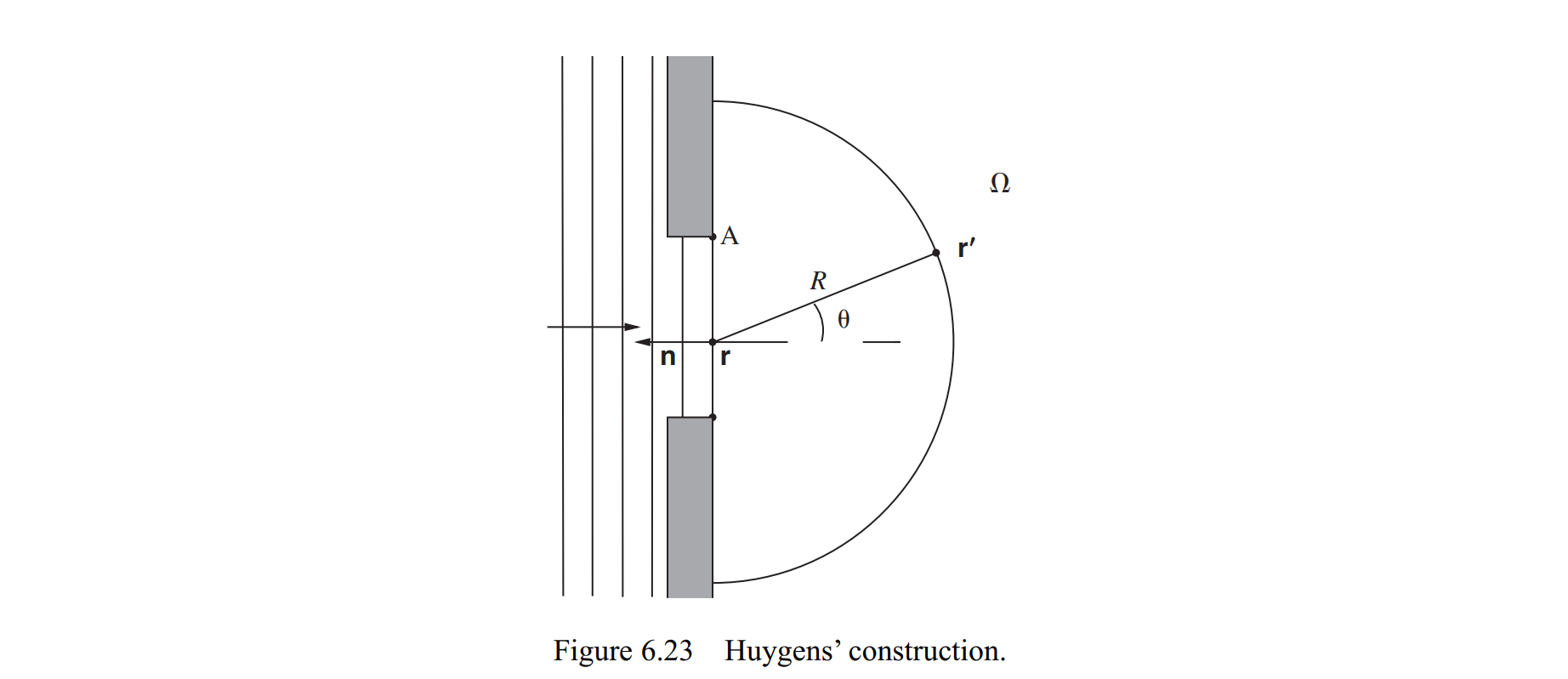
根据上图,其在小孔处的梯度是$-i k e^{i k x}$。在距离小孔的距离远大于波长的地方,可以近似
$\nabla_{\mathbf{r}} G\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \approx \frac{ik}{4\pi} \frac{\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{2}} e^{i k\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}$
代入,就知道
$\psi\left(\mathbf{r}^{\prime}\right) \approx \frac{k}{4 \pi i} \int_{\text {aperture }} \frac{e^{i k\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}(1+\cos \theta) d S_{\mathbf{r}}$
于是乎,因子$K\propto(1+cos\theta)$。这就是基尔希霍夫得出的修正因子。现在,新的“菲涅尔-基尔希霍夫”原理告诉我们两个惠更斯没有指出的事情:
- 波阵面往前产的波大于往回产的波。
- 分母的i给出一个90度的相位差,这是实验证实了的。对于这一点,如果不做计算,即使是惠更斯,恐怕也想不到吧