week 9,10
气氛突然数学起来。
这次讲的基本上就是张量——张量积,张量的分解(CP-Decomposition, HOSVD)。之前我们处理矩阵,用的是SVD和eigenset的分解,动机是在低维上把握矩阵的行为,进而把握这些矩阵对应的高维数据集的性质。对于张量,很容易想到如法炮制。但是不幸的是,尽管矩阵的分解是一个相对容易的套路,张量的decomposition却是一个NP-hard的问题。
何为张量
有三种定义。
- free vector space中的等价类。——QM里面,用的是这个定义。我们在这个讲义里用的也是这个定义。
- basis变换时满足某种特定变换规则的对象。——GR里面我学到的就是这个。这也是我在课上唯一听懂的部分。
- “linearizer of multilinear maps”——一个数学家可能会喜欢的说法。与本课的内容和我的兴趣都无关。
对于我不幸的大脑来说,这些定义都太数学了。况且,我不像许多其他同学一样学过许多高明的量子场论。因此,在了解这些定义的具体内容之前,不妨先产生一个模糊的概念:张量是线性映射之间的线性映射。
第一个定义的解释
取$n_{1}, \dots, n_{k}$维欧氏空间$V_{1}, \ldots, V_{k}$,令$\mathcal{F}$代表这些空间的cartesian积生成的所谓"free vector space",这就是说,Cartesian积得到的$\sum n_i$维空间中的每一个元素都是该空间的一个basis(现在,忘掉直和空间中的线性性)。一开始,我还以为$V_{1} \times V_{2} \times \ldots \times V_{k}$就是$\mathcal{F}$呢。实际上,Cartesian Product弄出来的这东西叫直和,维数是$\sum n_i$;直积得到的空间,维数是$\prod n_i$。
令$\mathcal{M}$是由形如
$\left(x_{1}, \ldots, x_{i-1}, x_{i}+y_{i}, x_{i+1}, \ldots, x_{k}\right)-\left(x_{1}, \ldots, x_{i-1}, x_{i}, x_{i+1}, \ldots, x_{k}\right)-\left(x_{1}, \ldots, x_{i-1}, y_{i}, x_{i+1}, \ldots, x_{k}\right)$
和
$\alpha\left(x_{1}, \ldots, x_{i-1}, x_{i}, x_{i+1}, \ldots, x_{k}\right)-\left(x_{1}, \ldots, x_{i-1}, \alpha x_{i}, x_{i+1}, \ldots, x_{k}\right)$
的元素构成的子空间。那么,直积$V_{1} \otimes \cdots \otimes V_{k}$就是商空间$\mathcal{F} / \mathcal{M}$。商空间的意思就是说,对于$\mathcal{F}$中的元素F, f,$F=f+m,m\in\mathcal{M}$,那么这两个元素属于同一个等价类,这些等价类的集合就是商空间。一个简单的例子。取$V_1$,$V_2$。他们的基是$\{v_k\}$,$\{w_k\}$。$V_1\times V_2$的基底是$\{(v_i,0)+(0,w_j)\}$。$V_1\otimes V_2$的基底是$\{(v_i, w_j)\}$。
为什么说这个定义是QM里面采用的呢?在QM里面,量子态的直积满足以下性质:
$\psi_1\otimes(\phi_1+\phi_2)=\psi_1\otimes\phi_1+\psi_1\otimes\phi_2; \alpha\psi\otimes\phi=\psi\otimes(\alpha\phi)=\alpha(\psi\otimes\phi)$
此处等号就表示属于同一个等价类。
第二个定义的解释
取V有基$\left\{e_{1}, \ldots, e_{n}\right\}$,其对偶空间有$\left\{e^{* 1}, \ldots, e^{* n}\right\}$ 满足 $e^{* j}\left(e_{i}\right)=\delta_{i}^{j}$。现在,我们旋转一下,将V的基换成$\tilde{e}_{k}=\sum_{i=1}^{n} A_{k}^{i} e_{i}$。或者说,$e_{i}=\sum_{k=1}^{n}\left(A^{-1}\right)_{i}^{k} \tilde{e}_{k}$。
我们可以知道,$\tilde{e}^{* \ell}=\sum_{j=1}^{n}\left(A^{-1}\right)_{j}^{\ell} e^{* j}$。对偶空间基底的变化是A的逆决定的。这种变化方式与V的基底的变化方式相逆,因此称这是逆变的。
对于V中向量v,
$\sum_{i=1}^{n} \sum_{k=1}^{n} v^{i}\left(A^{-1}\right)_{i}^{k} \tilde{e}_{k}=\sum_{k=1}^{n} \tilde{v}^{k} \tilde{e}_{k} \Rightarrow\tilde{v}^{k}=\sum_{i=1}^{n}\left(A^{-1}\right)_{i}^{k} v^{i}$
其分量值的变化也是逆变的。
对于对偶空间中向量w的分量,自然是协变(与V的基底的变化方式协同)的:$\tilde{w}_{\ell}=\sum_{j=1}^{n} A_{\ell}^{j} w_{j}$。
因此,我们可以写出张量的分量的变化规律来:
$\tilde{t}_{\ell_{1} \cdots \ell_{q}}^{k_{1} \cdots k_{p}}=\left(A^{-1}\right)_{i_{1}}^{k_{1}} \cdots\left(A^{-1}\right)_{i_{p}}^{k_{p}} A_{\ell_{1}}^{j_{1}} \cdots A_{\ell_{q}}^{j_{q}} t_{j_{1} \cdots j_{q}}^{i_{1} \cdots i_{p}}$
考虑一个矩阵M,它是两个线性空间之间的线性映射。现在这两个空间的基底都旋转:
$\tilde{e}_{k}=\sum_{j=1}^{n} A_{k}^{j} e_{j}$ ; $\tilde{f}_{\ell}=\sum_{i=1}^{m} B_{\ell}^{i} f_{i}$
如果我们把M的分量写成$M^i_j$的形式,$M\left(e_{j}\right)=\sum_{i=1}^{m} M_{j}^{i} f_{i}$,那么
$\begin{aligned} M\left(\tilde{e}_{k}\right) &=M\left(\sum_{j=1}^{n} A_{k}^{j} e_{j}\right)=\sum_{j=1}^{n} A_{k}^{j} M\left(e_{j}\right)=\sum_{j=1}^{n} A_{k}^{j}\left(\sum_{i=1}^{m} M_{j}^{i} f_{i}\right) \\ &=\sum_{i=1}^{m} \sum_{j=1}^{n} M_{j}^{i} A_{k}^{j} f_{i}=\sum_{\ell=1}^{m}\left(\sum_{i=1}^{m} \sum_{j=1}^{n}\left(B^{-1}\right)_{i}^{\ell} M_{j}^{i} A_{k}^{j}\right) \tilde{f}_{\ell} \end{aligned}$
顺理成章。
因此,M的变换方式正是(1,1)张量的变换方式,M可以认为是$W \otimes V^{*}$的一个元素了。
张量积空间的一些情形
$V^{*} \otimes W$和$W \otimes V^{*}$是一样的。这就是说,ij的前后顺序没什么关系。为了理解这个事实,我们引入张量积作为向量的写法,因为张量积空间是向量空间,这是很自然的。将两个向量的张量积记成:
$a \otimes b=\left(\begin{array}{c}{a^{1} b} \\ {a^{2} b} \\ {\vdots} \\ {a^{n_{1}} b}\end{array}\right)$
现在有线性映射$A: V_{1} \rightarrow W_{1}$ and $B: V_{2} \rightarrow W_{2}$。我们知道,$A\otimes B$作用在$V_1$中元素和$V_2$中元素的张量积上,得到$(A \otimes B)(a \otimes b)=(A a) \otimes(B b)$。在这种记号之下,
$A \otimes B=\left(\begin{array}{cccc}{A_{11} B} & {A_{12} B} & {\cdots} & {A_{1 n_{1}} B} \\ {A_{21} B} & {A_{22} B} & {\cdots} & {A_{2 n} B} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {A_{m_{11} B}} & {A_{m_{12}} B} & {\cdots} & {A_{m_{1 n 1}} B}\end{array}\right)$
这是很令人满意的。这种矩阵运算也叫矩阵的Kronecker积。特别的,可以想见,取$M=A\otimes B$,取A和B的standard basis(即cartesian basis),显然有
$f_{i} \otimes e^{* j}=f_{i}\left(e_{j}\right)^{t}$
$e^{* j} \otimes f_{i}=f_{i}\left(e_{j}\right)^{t}$
(根据$W\otimes V^*$的意思,$M_{j}^{i} f_{i} \otimes e^{* j}=M$)
因此本节初提到的两个张量积空间是相等的。
张量的缩并
$T_{q}^{p}=V_{1} \otimes \cdots \otimes V_{p} \otimes W_{1}^{*} \otimes \cdots \times W_{q}^{*}$
取$v^{(i)} \in V_{i}$,$\varphi^{(j)} \in W_{j}^{*}$,定义线性映射$C_{s}^{r}: T_{q}^{p} \longrightarrow T_{q-1}^{p-1}$,那么映射
$C_{s}^{r}\left(v^{(1)} \otimes \cdots \otimes v^{(p)} \otimes \varphi^{(1)} \otimes \cdots \otimes \varphi^{(q)}\right)=\varphi^{(s)}\left(v^{(r)}\right) v^{(1)} \otimes \cdots v^{(\hat{r})} \cdots \otimes v^{(p)} \otimes \varphi^{(1)} \otimes \cdots \varphi^{(\hat{s})} \cdots \otimes \varphi^{(q)}$
是缩并映射。其中,带帽子的指标表示在直积中略去这一项。
张量的秩
张量积空间也是向量空间,所以张量积之间还可以继续张量积。取$t \in T_{q}^{p}$,$s \in T_{s}^{r}$,我们记
$\begin{aligned} T_{q}^{p} & \times T_{s}^{r} \rightarrow T_{q}^{p} \otimes T_{s}^{r} \\(t, s) & \mapsto t \otimes s \end{aligned}$
由上一节的结论,我们可以shuffle所有那些一维的向量空间,从而得到$T_{q}^{p} \otimes T_{s}^{r} \cong T_{q+s}^{p+r}$。
授课者的remark:由此,我们可以建立张量代数$T(V)=\bigoplus_{p=0}^{\infty} T^{p}(V)$,从而进入数学家熟悉的领域。
令$t \in T^{p}=V_{1} \otimes \cdots \otimes V_{p}$,那么定义张量秩
$\operatorname{rank}(t)=\arg \min _{r}\left\{r \in \mathbb{N} | t=\sum_{i=1}^{r} v_{(i)}^{(1)} \otimes \cdots \otimes v_{(i)}^{(p)}, \text { where } v_{(i)}^{(j)} \in V_{j}\right\}$
与矩阵秩意义差不多,都是用尽可能少的秩为一的分量刻画一个线性映射。所以说一个秩为一的(p,0)张量就是p个向量的张量积(用上一节的符号写下来,还是一个向量的样子)。
一般张量的秩的计算是NP-hard问题。常用的算法是CP(canonical polyadic) decomposition。我们之后会再提到它。张量的情况里,我们同样希望做低秩的近似。有一种叫Kruskal记号的,是这样做的:$\lambda \in \mathbb{R}^{k}$,$U^{(n)} \in \mathbb{R}^{I_{n} \times k}$,$i=1, \ldots, p$,记
$[\lambda ; U^{(1)}, \ldots, U^{(p)}] \equiv \sum_{j=1}^{k} \lambda_{j} u_{(j)}^{(1)} \otimes \cdots \otimes u_{(j)}^{(p)}$
$I_n$是一个数列,表示每个U矩阵的行数。每个U矩阵都有k列,并且规定它们全是$l_2$-norm为1的。$u_{(j)}^{(i)}$就是第i个U矩阵的第j列。一般来说,固定k,$\mathcal{Y} \in V_{1} \otimes \cdots \otimes V_{p}$,其中$\operatorname{dim}\left(V_{n}\right)=I_{n}$。然后我们找具体的$\lambda$和$U$,使得$\mathcal{Y} \approx \mathcal{X} \equiv [\lambda ; U^{(1)}, \ldots, U^{(p)}]$。比如说我们熟悉的SVD就可以写成$[\sigma; U, V]$。
这里约等于的意思还不明确。我们通过定义张量上的距离来解决这个问题。例如,Frobenius内积
$\langle t, s\rangle_{F}=\sum_{i_{1}, \ldots, i_{p}} t^{i_{1} \ldots i_{p}} s^{i_{1} \ldots i_{p}}$。
Tensor Embedding of Vectorial Data
量子力学里面,人们关心张量积,是因为想要分解一个复杂系统的波函数,分离出它的自由度来。固体物理最近的一些进展使得人们产生了如下的想法:把n维欧氏空间的数据点表示成张量$t^{i_{1} \cdots i_{p}}$,那么
$\hat{y}=w_{i_{i} \cdots i_{p}} t^{i_{1} \cdots i_{p}}$
就是一个predictor。这个weight tensor元素太多,一般是通过分解成低秩张量来近似求解。据这课的老师讲,那些固体物理学家盯上了一个叫TT decomposition的东西,原理是把高秩的w压缩成一些矩阵,减少需要优化的参数的数目。
还有另外一个故事(思路),这就是把张量积空间当做是普通的线性空间,然后用我们熟悉的线性空间的工具来处理。例如,考虑一个embedding
$\left(\begin{array}{l}{x} \\ {y}\end{array}\right) \mapsto\left(\begin{array}{c}{\cos \frac{\pi x}{4}} \\ {\sin \frac{\pi x}{4}}\end{array}\right) \otimes\left(\begin{array}{c}{\cos \frac{\pi y}{4}} \\ {\sin \frac{\pi y}{4}}\end{array}\right) \in \mathbb{R}^{2} \otimes \mathbb{R}^{2}$
考虑一个如下图左上角的数据
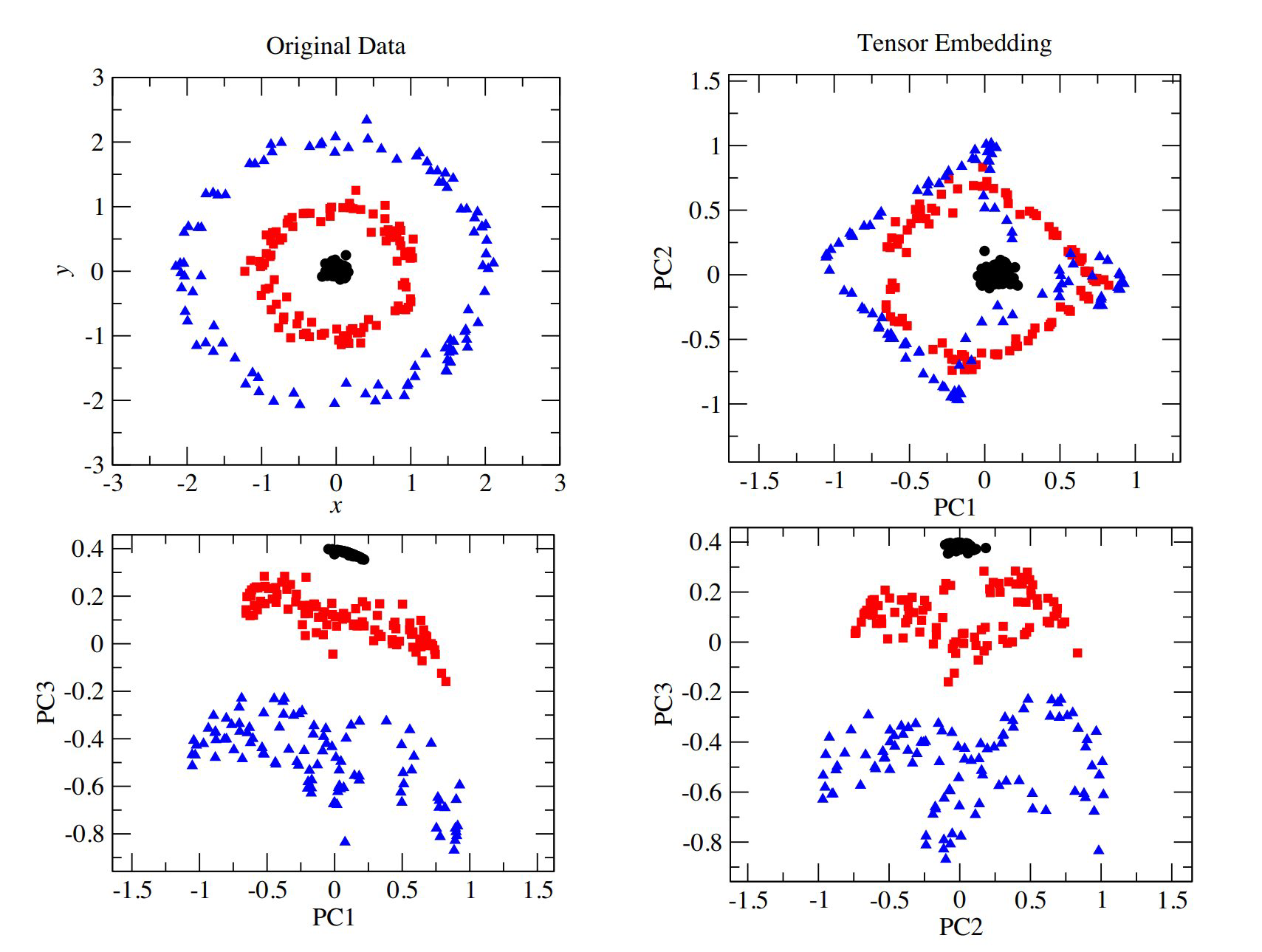
x值接近0的点会产生向量$\left(\begin{array}{l}{1} \\ {0}\end{array}\right)$,而$x\sim\pm1$的点会产生$\left(\begin{array}{c}{0} \\ {\pm 1}\end{array}\right)$。y也一样。如图下方,在张量积第1,3个分量的图中,这些点恰当地分开了。
Symmetric and Alternating tensors
令$\pi_{p}$是置换群。取其元素$\sigma$,作用在$T^{p}(V)$的分量上,
$\sigma(t)=t^{i_{\sigma(1)}, \ldots, i_{\sigma(p)}} e_{i_{1}} \otimes \cdots \otimes e_{i_{p}}$
如果$\forall \sigma \in \pi_{p}$,$\sigma(t)=t$,那么就说这个tensor是symmetric的;如果$\forall \sigma \in \pi_{p}$,$\sigma(t)=\operatorname{sign}(\sigma) t$,那就是alternating的。所有(p,0)的symmetric 的张量的集合写作$\operatorname{Sym}^{p}(V)$ 或$S^{p}(V)$,alternating的则写作$\bigwedge^p(V)$。
什么是tensor unfolding
取$t \in V_{1} \otimes \cdots \otimes V_{p}$。在分量记号下,$t^{i_{1} \cdots i_{p}}$所有n-th index的集合叫做第n个模。例如,取
$t=\left(\begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6}\end{array}\right)$
那么第一个模就是行指标1,2,第二个模就是列指标1,2,3.
然后,固定一个mode,变化其他所有的指标,得到的就是mode-n fibre。比如说,
令$t \in V_{1} \otimes \cdots \otimes V_p$,$I_i$是$V_i$的维数。那么t的mode-n unfolding/matricization/flattening 就是一个$I_{n} \times\left(\prod_{i \neq n} I_{i}\right)$维的矩阵,记做$\mathbf{t}_{(n)}$,其中原张量分量$t^{i_{1} \cdots i_{p}}$被map到矩阵的第$i_n$行,j列,其中
$j=1+\sum_{\ell=1, \ell \neq n}^{p}\left[\left(i_{\ell}-1\right) J_{\ell}\right]$
$J_{\ell}=\left\{\begin{array}{cl}{\prod_{m=\ell+1}^{n-1} I_{m},} & {\ell \leq n-2} \\ {1,} & {\ell=n-1} \\ {\prod_{r=1}^{n-1} I_{r} \prod_{s=\ell+1}^{p} I_{s},} & {\ell \geq n+1}\end{array}\right.$
**这玩意到底是什么意思?**我到现在也不知道。这种充满指标的公式对我来说是不可理解的。我只能拿一个性质当做定义来理解,即
$\mathbf{X}_{(n)}=v_{n}\left(v_{n+1} \otimes \cdots v_{p} \otimes v_{1} \otimes \cdots v_{n-1}\right)^{t}$
所以说,行数是指标$i_n$决定的,而至于每一列怎么排,那就是先紧着$i_{n+1}$排,然后是$i_{n+2}$,一直到$i_p$,再是$i_1$,然后再到$i_{n-1}$。根据我看到的资料,这个顺序好像不是什么物理意义之类的东西决定的,而是Fortran的习惯。
n-mode product
$\mathcal{X} \in V_{1} \otimes \cdots \otimes V_{p}$,$A=W \otimes V_{n}^{*}$,那么矩阵A从张量(把它想象成一个高维数阵立方体)的第n个维度上乘过去,就是
$\mathcal{Y} \equiv \mathcal{X} \times_{n} A=C_{1}^{n}(\mathcal{X} \otimes A)$
从这个角度想,$\mathcal{Y}=\mathcal{X} \times_{n} A \Longleftrightarrow \mathbf{Y}_{(n)}=\mathbf{A} \mathbf{X}_{(n)}$就是显然的了。如果$\mathcal{Y}=\mathcal{X} \times_{1} U_{1} \times_{2} U_{2} \times_{3} \cdots \times_{p} U_{p}$,那么flattening就可以相应地写成$\mathbf{Y}_{(n)}=U_{n} \mathbf{X}_{(n)}\left(U_{n+1} \otimes \cdots \otimes U_{p} \otimes U_{1} \otimes \cdots \otimes U_{n-1}\right)^{t}$。
CP decomposition
这玩意叫canonical,主要原因是它是从tensor rank的定义出发的。但是实际上哪怕是对矩阵这种低阶张量的分解也不是这样做的:我们是做SVD,动用一个稀疏的“core tensor”或者说singular value matrix,来分担这个矩阵在空间上多么“椭”的信息,而不是拿几个矩阵乘积加权求和去得到原矩阵(这种做法相当于使用identity作core tensor)。
CP decomposition唯一的优势是它简单。算法上,它是这样做的:首先,定义Khatri-Rao product
$A \odot B=\left(A_{; 1} \otimes B_{; 1} \cdots A_{:, K} \otimes B_{:, K}\right)$
现在有$\mathcal{Y}\in V_{1} \otimes \cdots \otimes V_{p}$,想拿$\mathcal{X}=[ \lambda ; U^{(1)}, \ldots, U^{(p)} ]$去套它,判断标准采用frobenius norm。我们首先固定所有的U,只留一个$U^{(n)}$来优化。为了方便起见,采用unfolding出来的矩阵,这样比较好处理:
$\mathbf{X}_{(n)}=U^{(n)} \Lambda\left(U^{(n+1)} \odot \cdots \odot U^{(p)} \odot U^{(1)} \odot \cdots \odot U^{(n-1)}\right)^{t}$
解$\min _{A}\left\|\mathbf{Y}_{(n)}-A\left(U^{(n+1)} \odot \cdots \odot U^{(p)} \odot U^{(1)} \odot \cdots \odot U^{(n-1)}\right)^{t}\right\|_{F}^{2}$
令$A=U^{(n)} \Lambda$,$B=\left(U^{(n+1)} \odot \cdots \odot U^{(p)} \odot\right.\left.U^{(1)} \odot \cdots \odot U^{(n-1)}\right)$
那么就可以用MP伪逆求得
$A\left(B^{t} B\right)=\mathbf{Y}_{(n)} B \Rightarrow A=\mathbf{Y}_{(n)} B\left(B^{t} B\right)^{+}$
那么,$\lambda$就是A的每一列的模,$U^{(n)}$就是A的每一列归一化之后得到的矩阵。
如此这般,先随机搞一批U,然后一个一个地优化。这个方法很令人不舒服,因为它是ill-posed的,不能保证收敛。
HOSVD(high order SVD)
这是低维的SVD在高维的推广,也叫tucker decomposition,但tucker本人只是搞了三维的情况。现在令$I_n$是每个$V_n$的维数,那么$\mathcal{X} \in V_{1} \otimes \cdots \otimes V_{p} \equiv T^{p}$可以被分解成
$\mathcal{X}=\mathcal{S} \times_{1} U^{(1)} \times_{2} U^{(2)} \cdots \times_{p} U^{(p)}$
比如说,对于一个矩阵,$M=\Sigma\times_1U\times_2 V$。
我个人理解这个S是sparse,不是singular。可能是因为我从来就没理解singular value这个名字到底啥意思。sparse不仅是说S“只有对角元”,也说明这个新东西参数少。还是拿矩阵的SVD来说,本来T的维数是$m\times n$,现在有$k\ll m,n$个奇异值,那么只需要$k(m+n-1)\ll mn$个参数就能刻画整个矩阵。
这个S也满足矩阵的奇异值分解的诸般性质。比如
- $U^{(n)}=\left(U_{(1)}^{(n)} \cdots U_{\left(I_{n}\right)}^{(n)}\right)$是$I_{n} \times I_{n}$的正交矩阵;
- $\forall n \in\{1, \ldots, p\},\left\langle S^{i n=\alpha}, S^{i_{n}=\beta}\right\rangle_{F}=0$ for $\alpha \neq \beta$,S的“列”互相正交;
- $\left\|S^{i_{n}=1}\right\|_{F} \geq \cdots \geq\left\|S^{i_{n}=I_{n}}\right\|_{F} \geq 0$,S的“列”可以排序。
怎么求这个分解呢?我们可以对unfolding得到的矩阵做SVD:
$\mathbf{X}_{(n)}=U^{(n)} \Sigma^{(n)} V^{(n)^{t}}$
顺手排序:
$\sigma_{1}^{(n)} \geq \sigma_{2}^{(n)} \cdots \geq \sigma_{I_{n}}^{(n)} \geq 0$
然后用这个$U^{(i)}$定义
$S=\mathcal{X} \times_{1} U^{(1)^{t}} \times_{2} U^{(2) t} \cdots \times_{p} U^{(p)^{t}}$
这样就都求出来了。这样得到的结果自然满足以上性质,例如后两条(第一条是平凡的)
$\begin{aligned} \mathbf{S}_{(n)} &=U^{(n) t} \mathbf{X}_{(n)}\left(U^{(n+1)^{t}} \otimes \cdots \otimes U^{(p) t} \otimes U^{(1)^{t}} \otimes \cdots \otimes U^{(n-1)^{t}}\right)^{t} \\ &=U^{(n)^{t}} \mathbf{X}_{(n)}\left(U^{(n+1)} \otimes \cdots \otimes U^{(p)} \otimes U^{(1)} \otimes \cdots \otimes U^{(n-1)}\right) \\&=\Sigma^{(n)} V^{(n)^{t}}\left(U^{(n+1)} \otimes \cdots \otimes U^{(p)} \otimes U^{(1)} \otimes \cdots \otimes U^{(n-1)}\right)\end{aligned}$
从这里能看出来,那一串U是正交变换,所以S的orthogonality是V决定的,V自然满足这性质。然后$\left\|S^{i_{n}=1}\right\|_{F}=\sigma_1^{(n)}$,以此类推,所以排序必然成立。这样,所有性质都满足。
TTSVD
所谓Tensor Train SVD,指的是把张量的每个分量用一连串矩阵相乘的形式表示的操作。附图中,TTSVD的记号长得像一列火车,因此得名。我对这个东西的理解不是很好,所以简要记之,以后再想。
$A\left(i_{1}, i_{2}, \ldots, i_{p}\right)=G_{1}\left(i_{1}\right) G_{2}\left(i_{2}\right) \ldots G_{p}\left(i_{p}\right)$
其中$G_{k}\left(i_{k}\right)$ 是 $R_{k-1} \times R_{k}$的一族矩阵(换句话说,$G_k$是一个$V^{R_{k-1}}\otimes V^{R_k}\otimes V^{I_k}$的张量)。由“边界条件”,$r_0=r_{p}=0$。算法是这样的:从$i_1$这维度unfold,做SVD,然后得到$U_1$,这是一个$1\times I_1\times R_1$的数阵。接着,对SVD右面的$\Sigma V$部分做unfolding,同时unfold$r_1$和$i_2$两个维度,再做SVD,得到$U_2$,这是一个$(R_1\times I_2)\times R_2$的矩阵……通过这种方式,我们就可以从$U$得出$G$来。
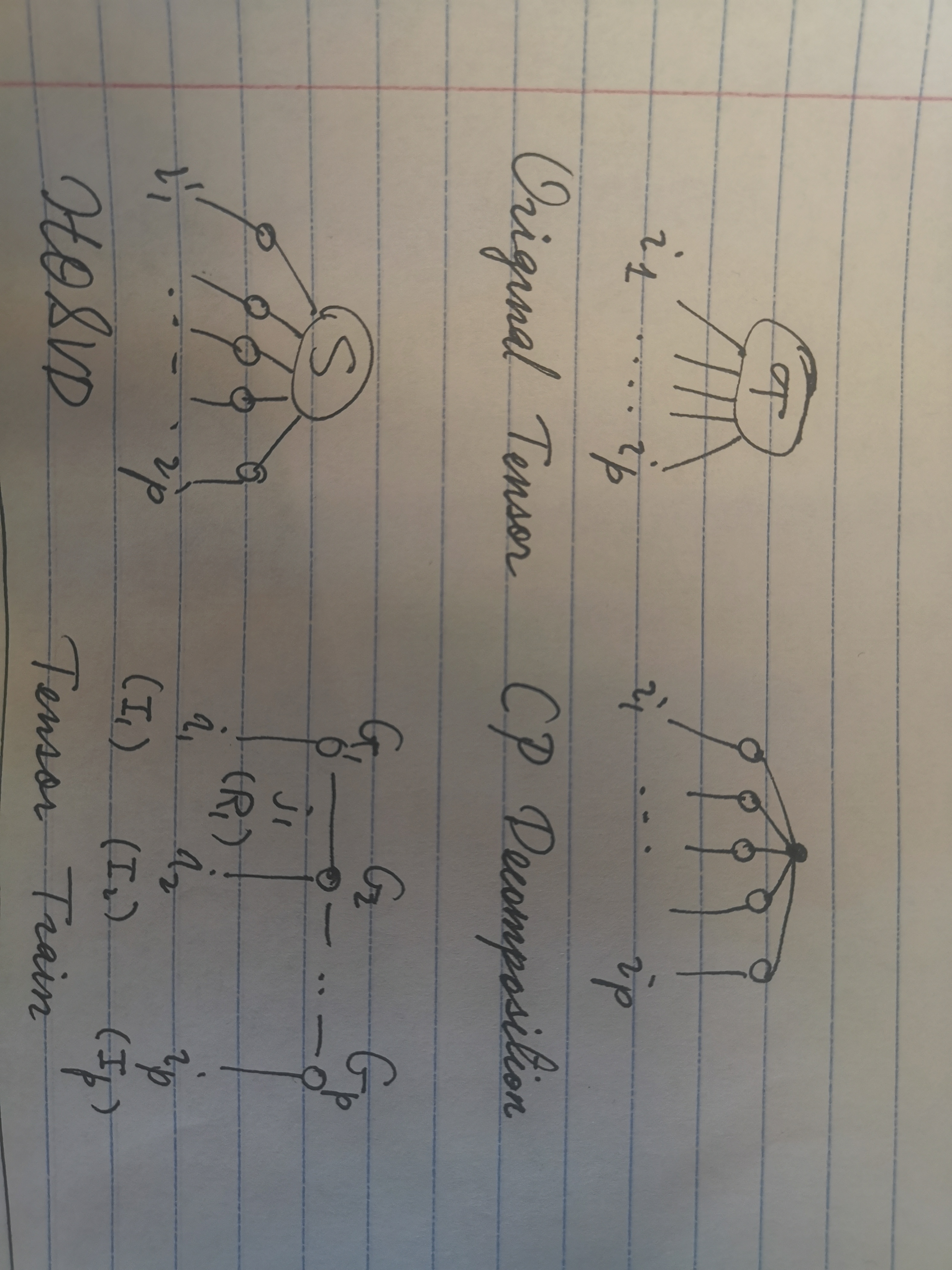
(三种decomposition方法的图示)
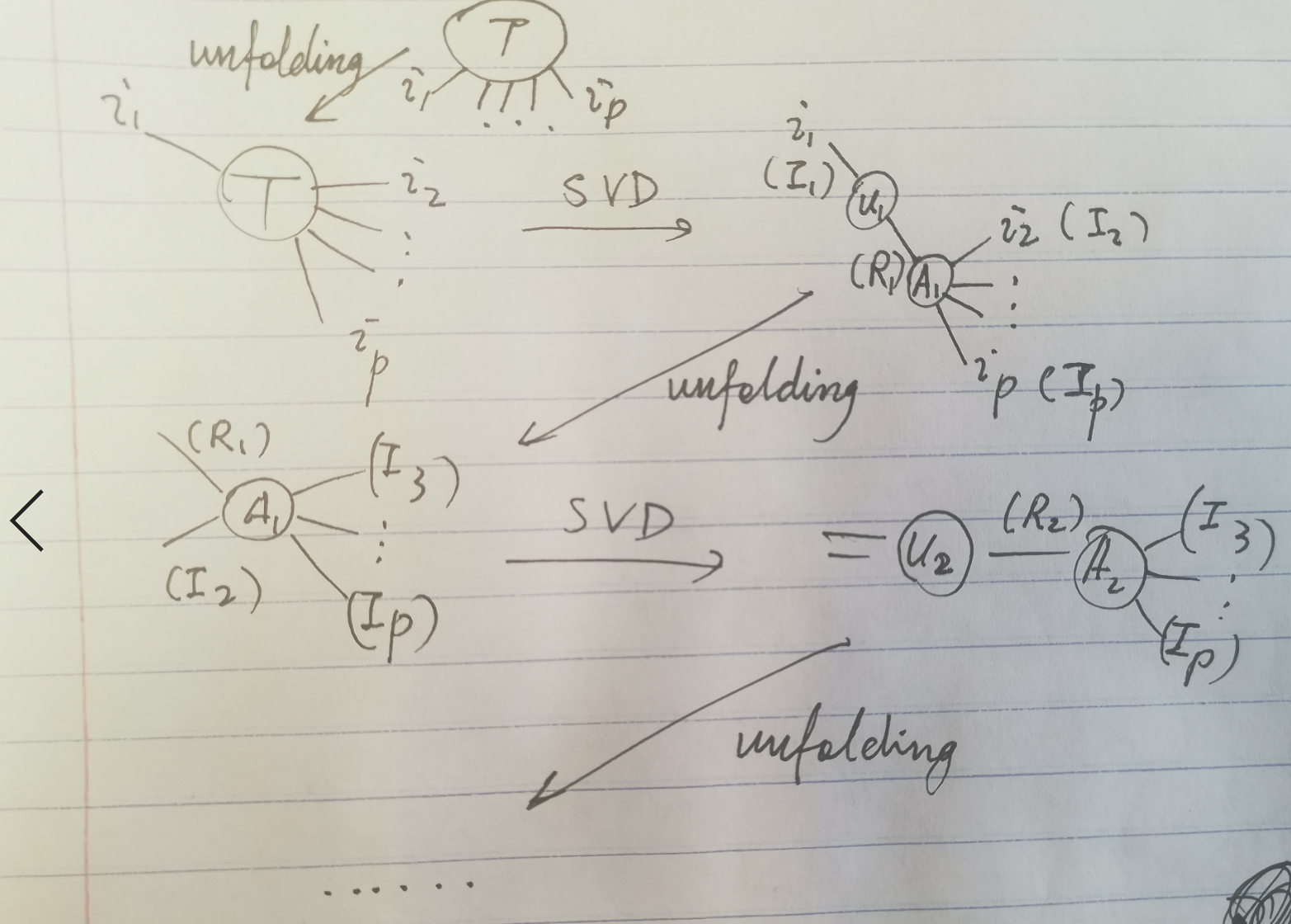
(tensor train SVD细节